RBF神经网络python实践学习（BP算法）

续上一篇：RBF神经网络学习及实践

RBF神经网络求解方法

RBF网络中需要求解的参数为：径向基函数的中心、方差和隐层到输出层的权值。

对于基函数中心的选取方法主要有：随机选取、聚类选取、有监督学习选取。对于方差计算方法有：直接公式计算、有监督学习修正计算。权值计算方法有：伪逆法直接求解、最小二乘法直接求解、有监督学习修正求解。

在上一篇的python代码实现中，我们采用直接计算法求解参数。即随机在样本中选取一定数量（即隐层神经元数量）的个体作为径向基函数的中心，且中心自此固定下来，隐层神经元输出便是已知，最终权值直接通过求解线性方程组确定即可。但这种方法的适用前提是样本数据分布具有代表性，否则会导致回归效果不佳。

其次，对于基函数中心选取也有通过聚类（一般采用K-Means）实现，方程由下面公式计算：
$$\sigma =\frac{d_{\max }}{\sqrt{2n}}$$
其中 $d_{max}$ 为聚类得到的中心之间的最大距离，$n$ 为中心数量。

相较于随机选取，聚类方法更能使中心的选取具有代表性。

本文将学习如何使用有监督学习算法对RBF网络参数进行训练，即对损失函数（一般使用MSE）进行梯度下降，再修正每个参数。

定义了RBF网络后，定义损失函数（误差函数，这里使用均方误差MSE）如下：
$$E=\frac{1}{2m}\sum _{i=1}^m{e}_i^2=\frac{1}{2m}\sum _{i=1}^m(f(x)-y{)}^2=\frac{1}{2m}\sum _{i=1}^m{\left(\sum _{j=1}^q{w}_j.\phi \left(x,c_j\right)-y\right)}^2$$
我们的目标是最小化损失函数，即使模型预测结果与实际值尽可能逼近。利用BP算法反向传播误差，并利用梯度下降法分别求得RBF网络参数优化的方向。

1. 隐层到输出层的权值迭代公式
   $$\Delta w=\frac{\partial E}{\partial w}=\frac{1}{m}\sum _{i=1}^m(f(x)-y)\cdot \phi (x,c)=\frac{1}{m}\sum _{i=1}^m{e}_i\cdot \phi (x,c)$$
   $$w_{k+1}=w_k-\eta \cdot \Delta w$$
2. 隐含层的神经元（径向基函数）中心点迭代公式

$$\begin{array}{rl}& \Delta c_j=\frac{\partial E}{\partial c_j}=\frac{\partial E}{\partial \phi \left(x,c_j\right)}\cdot \frac{\partial \phi \left(x,c_j\right)}{\partial c_j}\\ & =\frac{1}{m}\sum _{i=1}^m(f(x)-y)w\cdot \frac{\partial \phi \left(x,c_j\right)}{\partial c_j}\\ & =\frac{1}{m}\sum _{i=1}^m(f(x)-y)w\cdot \phi \left(x,c_j\right)\cdot \frac{x-c_j}{{\sigma }_j^2}\\ & =\frac{1}{m\cdot {\sigma }_i^2}\sum _{i=1}^m(f(x)-y)w\cdot \phi \left(x,c_j\right)\cdot \left(x-c_j\right)\end{array}$$

$$c_{k+1}=c_k-\eta \cdot \Delta c$$
3. 方差（高斯核宽度）迭代公式
$$\begin{array}{rl}& \Delta {\sigma }_j=\frac{\partial E}{\partial {\sigma }_j}=\frac{\partial E}{\partial \phi \left(x,c_j\right)}\cdot \frac{\partial \phi \left(x,c_j\right)}{\partial {\sigma }_j}\\ & =\frac{1}{m}\sum _{i=1}^m(f(x)-y)w\cdot \frac{\partial \phi \left(x,c_j\right)}{\partial {\sigma }_j}\\ & =\frac{1}{m\cdot {\sigma }_j^3}\sum _{i=1}^m(f(x)-y)w\cdot \phi \left(x,c_j\right)\cdot {\Vert x_i-c_j\Vert }^2\end{array}$$
$${\sigma }_{k+1}={\sigma }_k-\eta \cdot \Delta \sigma$$

迭代公式中 $\eta$ 为学习率，对于RBF中不同参数分别设置不同的学习率。经过多轮迭代直至损失函数收敛，训练结束${}^{[1]}$。

对于上述三个参数的迭代，为避免学习率过大过小带来权值振荡或学习速度缓慢，可以在修正公式中增加一个动量项 $\alpha ,\alpha \in (0,1)$。 直观上理解就是要是当前梯度方向与前一步的梯度方向一样，那么就增加这一步的权值更新，要是不一样就减少更新。

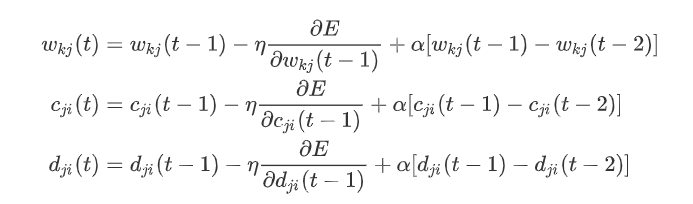
动量项参考：神经网络 动量因子

代码实现

python代码来源自参考文章${}^{[1]}$。

# -*- coding: utf-8 -*-
"""
Created on Sun Jul 12 19:15:20 2020
@author: ecupl
"""
import numpy as np
import matplotlib.pyplot as plt

class RBFnetwork(object):
    def __init__(self, hidden_nums, r_w, r_c, r_sigma):
        self.h = hidden_nums  # 隐含层神经元个数
        self.w = 0  # 线性权值
        self.c = 0  # 神经元中心点
        self.sigma = 0  # 高斯核宽度
        self.r = {"w": r_w,
                  "c": r_c,
                  "sigma": r_sigma}  # 参数迭代的学习率
        self.errList = []  # 误差列表
        self.n_iters = 0  # 实际迭代次数
        self.tol = 1.0e-5  # 最大容忍误差
        self.X = 0  # 训练集特征
        self.y = 0  # 训练集结果
        self.n_samples = 0  # 训练集样本数量
        self.n_features = 0  # 训练集特征数量

    # 计算径向基距离函数
    def guass(self, sigma, X, ci):
        return np.exp(-np.linalg.norm((X - ci), axis = 1) ** 2 / (2 * sigma ** 2))

    # 将原数据高斯转化成新数据
    def change(self, sigma, X, c):
        newX = np.zeros((self.n_samples, len(c)))
        for i in range(len(c)):
            newX[:, i] = self.guass(sigma[i], X, c[i])
        return newX

    # 初始化参数
    def init(self):
        sigma = np.random.random((self.h, 1))  # (h,1)
        c = np.random.random((self.h, self.n_features))  # (h,n)
        w = np.random.random((self.h + 1, 1))  # (h+1,1)
        return sigma, c, w

    # 给输出层的输入加一列截距项
    def addIntercept(self, X):
        return np.hstack((X, np.ones((self.n_samples, 1))))

    # 计算整体误差
    def calSSE(self, prey, y):
        return 0.5 * (np.linalg.norm(prey - y)) ** 2

    # 求L2范数的平方
    def l2(self, X, c):
        m, n = np.shape(X)
        newX = np.zeros((m, len(c)))
        for i in range(len(c)):
            newX[:, i] = np.linalg.norm((X - c[i]), axis = 1) ** 2
        return newX

    # 训练
    def train(self, X, y, iters, draw = 0):
        self.X = X
        self.y = y.reshape(-1, 1)
        self.n_samples, self.n_features = X.shape
        sigma, c, w = self.init()  # 初始化参数
        for i in range(iters):
            ## 正向计算过程
            hi_output = self.change(sigma, X, c)  # 隐含层输出(m,h)，即通过径向基函数的转换
            yi_input = self.addIntercept(hi_output)  # 输出层输入(m,h+1)，因为是线性加权，故将偏置加入
            yi_output = np.dot(yi_input, w)  # 输出预测值(m,1)
            error = self.calSSE(yi_output, y)  # 计算误差
            if error < self.tol:
                break
            self.errList.append(error)  # 保存误差
            ## 误差反向传播过程
            deltaw = np.dot(yi_input.T, (yi_output - y))  # (h+1,m)x(m,1)
            w -= self.r['w'] * deltaw / self.n_samples
            deltasigma = np.divide(
                np.multiply(np.dot(np.multiply(hi_output, self.l2(X, c)).T, (yi_output - y)), w[:-1]),
                sigma ** 3)  # (h,m)x(m,1)
            sigma -= self.r['sigma'] * deltasigma / self.n_samples
            deltac1 = np.divide(w[:-1], sigma ** 2)  # (h,1)
            deltac2 = np.zeros((1, self.n_features))  # (1,n)
            for j in range(self.n_samples):
                deltac2 += (yi_output - y)[j] * np.dot(hi_output[j], X[j] - c)
            deltac = np.dot(deltac1, deltac2)  # (h,1)x(1,n)
            c -= self.r['c'] * deltac / self.n_samples
            # 拟合过程画图
            if (draw != 0) and ((i + 1) % draw == 0):
                self.draw_process(X, y, yi_output)

        self.c = c
        self.w = w
        self.sigma = sigma
        self.n_iters = i

    # 画图
    def draw_process(self, X, y, y_prediction):
        plt.scatter(X, y)
        plt.plot(X, y_prediction, c = 'r')
        plt.show()

    # 预测
    def predict(self, X):
        hi_output = self.change(self.sigma, X, self.c)  # 隐含层输出(m,h)，即通过径向基函数的转换
        yi_input = self.addIntercept(hi_output)  # 输出层输入(m,h+1)，因为是线性加权，故将偏置加入
        yi_output = np.dot(yi_input, self.w)  # 输出预测值(m,1)
        return yi_output

测试代码

hidden_nums, iters = 20, 20000
X = np.linspace(-4, 4, 400)[:, np.newaxis]
y = np.multiply(1.1 * (1 - X + 2 * X ** 2), np.exp(-0.5 * X ** 2))
# y = np.sin(np.pi * X / 2) + np.cos(np.pi * X / 3)
# set y and add random noise
# y += np.random.normal(0, 0.1, y.shape)
rbf = RBFnetwork(hidden_nums, 0.1, 0.2, 0.1)
rbf.train(X, y, iters, draw = 50)
# 预测
plt.plot(X, y, 'r:')
plt.plot(X, rbf.predict(X), 'k')
print(rbf.c)
# plt.scatter(list(rbf.c), [0 for i in range(len(rbf.c))])
# plt.plot(rbf.errList)
plt.show()

测试结果分析和总结

• 超参数设置

  在BP（误差反向传播）训练中，学习率和隐层单元数等超参数的设置对训练过程及结果非常重要。较低的学习率会导致loss收敛缓慢，训练时间变长；较高的学习率则会导致loss振荡，甚至梯度爆炸。

  

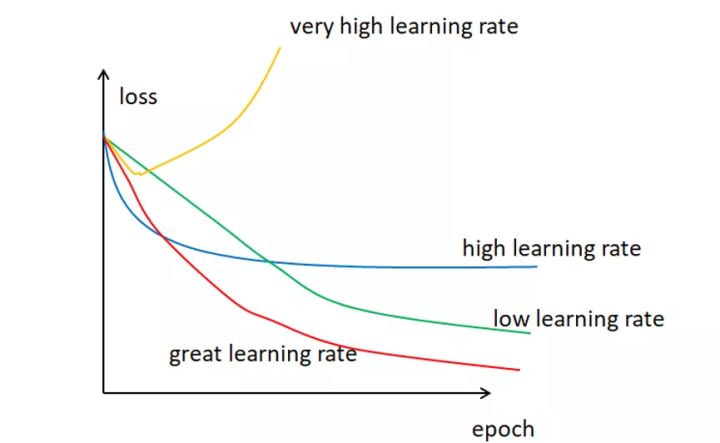
  对于隐层单元数的设置，数量过少会导致无法拟合复杂样本；数量过多会导致隐层输出矩阵尺寸变大，计算量增大。因此，合理的超参数设置很重要。在本测试代码中，可以通过观察误差曲线变化来增减学习率。后面，可以考虑使用粒子群算法等寻优算法对超参数选取进行优化。

• 参数初始化

  对于方差和权值，均采用[0,1)随机值初始化。

  sigma = np.random.random((self.h, 1))  # (h,1)
  w = np.random.random((self.h + 1, 1))  # (h+1,1)
  

  对于隐层中心，参照随机选取和聚类选用的思想，整个样本范围内的点作为中心的概率应当差不多。如果仍然采用[0,1)随机值，那么初始中心呈聚集状，学习率较低的情况下，需要多次迭代才能分散遍布样本空间。可以尝试在 $[x_{min},x_{max}]$ 区间内均匀随机初始化。

  c = np.random.uniform(-4, 4, (self.h, self.n_features))  # (h,n)
  

  当然，也可以尝试k-means聚类初始化中心。

• bias偏置单元

  在测试代码中，bias体现在给输入层的输入添加了一列截距项（全是1的一列）。与线性方程 $y=wx+b$ 中的 $b$ 的意义是一致的。在 $y=wx+b$ 中，$b$表示函数在y轴上的截距，控制着函数偏离原点的距离，在神经网络中的偏置单元也是类似的作用${}^{[2]}$。作用是使函数不过原点，让模型更加灵活。详见参考文章2。

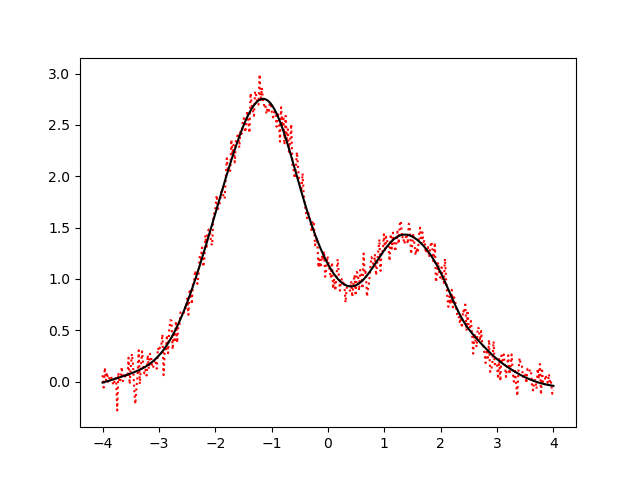
• 输入数据噪声敏感性

  从完全内插法的角度去理解RBF插值，即表面必须通过每一个测得的采样值。存在的问题就是当样本中包含噪声时，神经网络将拟合出一个错误的曲面，从而使泛化能力下降。但对于有监督训练的RBF神经网络，从测试结果可以看出，模型对输入噪声的敏感性不高。

  

• 多元线性回归矩阵求导

  当确定神经网络表达式后，即可确定相应的误差函数。使用梯度下降算法最小化误差函数中，求解参数迭代公式的重点便是矩阵求导。优化的参数不止一个，又是线性回归问题，故属于多元线性回归矩阵求导。相关学习资料详见参考3和参考4。

• 基函数中心不取自训练样本

  相比于随机和聚类选取后便固定不变的中心，有监督学习的RBF网络中基函数中心是BP修正参数，故在迭代过程中会不断变化，最终得到的中心参数可能不在训练样本范围内。

参考

[1] 机器学习算法推导&手写实现06——RBF网络 - 知乎 (zhihu.com)

[2] [转载]神经网络偏置项(bias)的设置及作用 - 别再闹了 - 博客园 (cnblogs.com)

[3] 矩阵求导术（上） - 知乎 (zhihu.com)

[4] 矩阵求导术（下） - 知乎 (zhihu.com)